28. Find the Index of the First Occurrence in a String

題目描述：

給定兩個字符串 haystack 和 needle，請在 haystack 字符串中找出 needle 字符串出現的第一個位置（下標從 0 開始）。如果不存在，則返回 -1。

Example:

• Input: haystack = "leetcode", needle = "leeto"
• Output: -1
• Explanation: "leeto" did not occur in "leetcode", so we return -1.

解題思路:
對於熟悉 JavaScript 的讀者來說，這道題目應該很容易聯想到 String 的 indexOf API，這個 API 的功能正是用來解決這個問題。然而，LeetCode 的意圖是讓我們思考如何自行實現這個功能，而不是直接使用現成的 API。儘管這道題目被標示為 Easy，但其實可以有不同程度的複雜解法。一般來說，追求越高效的解法，實現起來往往越複雜。

這裡我們介紹兩個解法。首先是暴力法，這種方法使用兩層迴圈：外層迴圈遍歷 haystack，內層迴圈遍歷 needle。當比較 haystack 和 needle 時，如果發現不一致，則外層迴圈的索引移動到下一個位置，然後繼續執行相同的流程。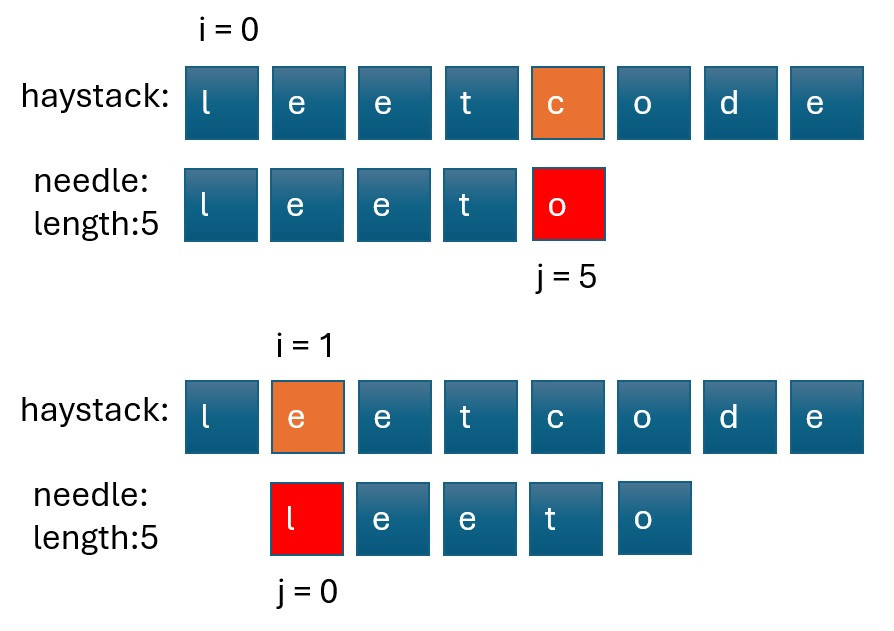

var strStr = function(haystack, needle) {
    if (needle === "") return 0;

    const n = haystack.length;
    const m = needle.length;

    for (let i = 0; i <= n - m; i++) {
        let j = 0;
        for (; j < m; j++) {
            if (haystack[i + j] !== needle[j]) {
                break;
            }
        }
        if (j === m) {
            return i;
        }
    }

    return -1;
};

時間複雜度：O(n * m)，在最壞的情況下，所有字符都需要進行比較，因此時間複雜度為 O((n - m + 1) * m)，可以簡化為 O(n * m)。
空間複雜度：O(1)，此算法只使用了一些額外的變數（如 n, m, i, j），這些都是常數級別的空間，因此空間複雜度為 O(1)。

另一種更高效的解法是使用哈希函數(hash function)。這個方法會先將字符串轉換成哈希值(hash value)，然後直接比較哈希值是否相同。如果哈希值不同，則說明這兩個字符串肯定不相同，可以直接排除。如果哈希值相同，則進一步進行逐字符比較，以確保兩個字符串確實相同。這種方法的優勢在於，它能夠通過一次哈希值的計算來快速排除大部分不匹配的情況，從而顯著提升效率。

剩下的問題是如何設計哈希函數來產生哈希值。最簡單的想法是將每個字符的 ASCII 值相加，從而產生哈希值。不過，這種方法有明顯的缺點：如果字符的位置改變但總數相同，結果的哈希值仍會相同。這樣的哈希函數會導致過多的哈希碰撞，從而降低搜尋效率。因此，為了提高效率，我們需要設計一個能夠有效區分不同字符串的哈希函數。

1987年，計算機科學家 Richard M. Karp 和 Michael O. Rabin 提出了 Rabin–Karp演算法，專門用來解決字符串匹配中的哈希碰撞問題。為了避免哈希碰撞，Rabin–Karp 的哈希函數將字符串中每個字符的位置納入考量。具體來說，每個字符的哈希值會是其 ASCII 值乘上一個 base 值，而這裡的 base 值通常取 256（因為 ASCII 是一個 byte）。此外，為了防止計算過程中出現 overflow，還需要對結果取模（mod）。這裡的 mod 通常選擇一個足夠大的質數，例如 (10^9 + 7)。通過這種方式計算得到的哈希值既均勻分佈，又不容易發生碰撞，從而提高了匹配的效率。
Rabin–Karp 哈希函數的另一個優點是，在需要重新計算哈希值時(rehash)，不必重新計算整個字符串的哈希值。相反，只需將最高位字符的哈希值去掉，然後加入新字符的 ASCII 值即可。這種滑動窗口式的計算方式極大地提高了效率，因為每次更新哈希值只涉及常數時間的操作，而不需要遍歷整個字符串。這也是 Rabin–Karp演算法在處理多次字串匹配時特別高效的原因之一。

function strStr(haystack, needle) {
    const n = haystack.length;
    const m = needle.length;
    if (m > n) return -1;

    const base = 256;  // 字母表的大小
    const mod = 10**9 + 7;  // 質數用來避免哈希值溢出
    let needleHash = 0;
    let haystackHash = 0;
    let highestPow = 1;

    // 計算 highestPow, 代表 base^(m-1) % mod
    for (let i = 0; i < m - 1; i++) {
        highestPow = (highestPow * base) % mod;
    }

    // 計算 needle 和 haystack 前 m 個字符的哈希值
    for (let i = 0; i < m; i++) {
        needleHash = (needleHash * base + needle.charCodeAt(i)) % mod;
        haystackHash = (haystackHash * base + haystack.charCodeAt(i)) % mod;
    }

    // 遍歷 haystack 中的每個可能的子字符串
    for (let i = 0; i <= n - m; i++) {
        // 比較哈希值，如果相同，則進行進一步的字符串比較
        if (needleHash === haystackHash) {
            if (haystack.slice(i, i + m) === needle) {
                return i;  // 如果匹配成功，返回當前索引
            }
        }

        // 滾動更新哈希值(rehash)
        if (i < n - m) {
            haystackHash = (haystackHash - haystack.charCodeAt(i) * highestPow) * base + haystack.charCodeAt(i + m);
            haystackHash = (haystackHash % mod + mod) % mod;  // 保持哈希值在模數範圍內
        }
    }

    return -1;  // 如果沒有找到匹配項，返回 -1
}

時間複雜度：O(n + m)，其中 n 是 haystack 的長度，m 是 needle 的長度。
空間複雜度：O(1)，主要是用來存儲哈希值和一些常數變量，不需要額外的空間。

總結:
透過這道 LeetCode 題目，我們可以深入思考 String 的 indexOf API 是如何實作的。無論是使用暴力法、Two Pointers，還是 Sliding Window 的方法，時間複雜度基本上都是 O(n * m)。然而，Rabin–Karp演算法可以將時間複雜度提升到 O(n + m)，且相較於其他進階演算法，Rabin–Karp演算法相對容易理解。因此，我將這道題目歸類為「Rabin–Karp演算法」。希望透過圖解的方式，能幫助讀者理解並學習這個演算法的核心精神。